← return to practice.dsc80.com
Instructor(s): Suraj Rampure
This exam was administered in-person. The exam was closed-notes, except students were allowed to bring two two-sided notes sheets. No calculators were allowed. Students had 180 minutes to take this exam.
The DSC 80 staff are looking into hotels — some in San Diego, for their family to stay at for graduation, and some elsewhere, for summer trips.
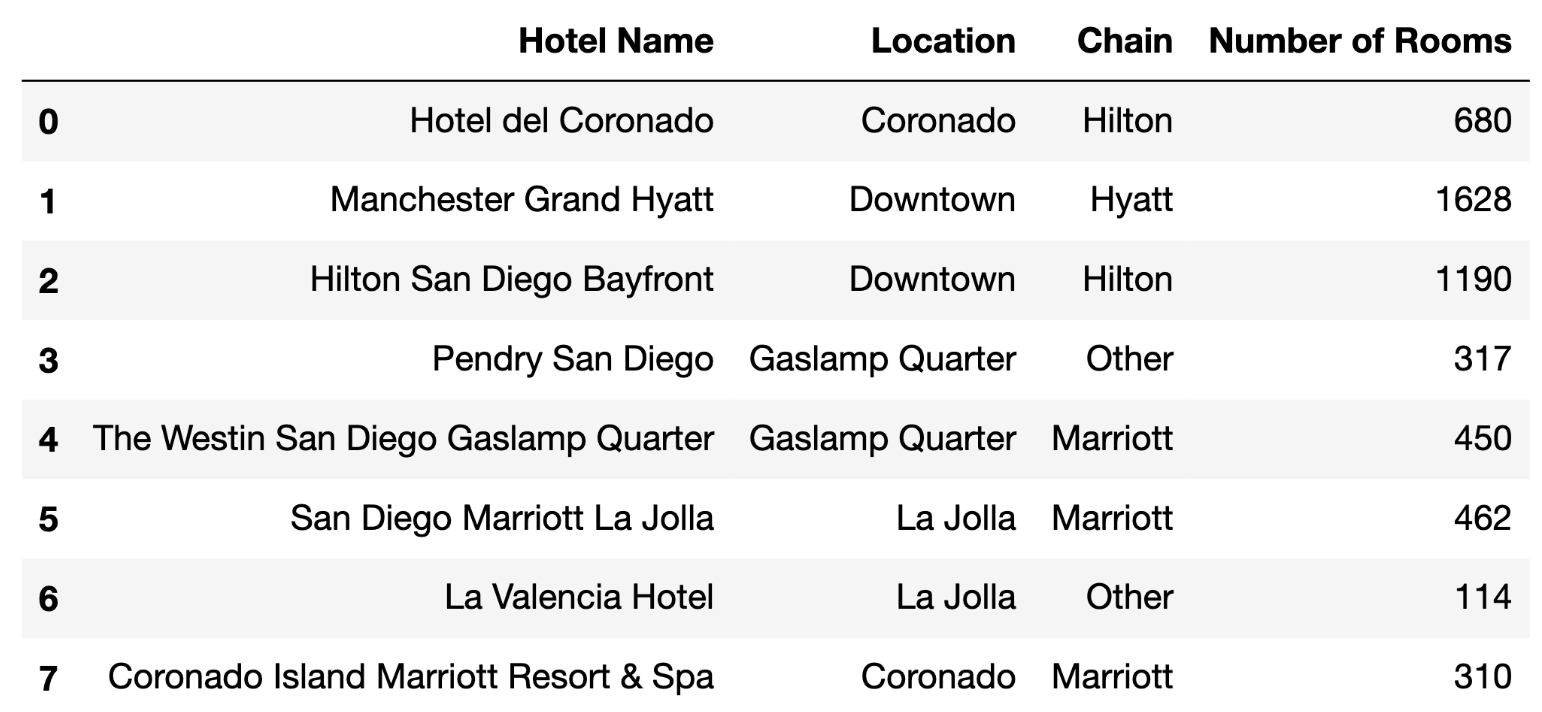
In Question 1 only, you will work with the DataFrame
hotels. Each row of hotels contains
information about a different hotel in San Diego. Specifically, for each
hotel, we have:
"Hotel Name" (str): The name of the hotel.
Assume hotel names are unique."Location" (str): The hotel’s neighborhood in San
Diego."Chain" (str): The chain the hotel is a part of; either
"Hilton", "Marriott", "Hyatt", or "Other". A hotel chain is
a group of hotels owned or operated by a shared company."Number of Rooms" (int): The number of rooms the hotel
has.The first few rows of hotels are shown below, but hotels
has many more rows than are shown.

Remember that hotels is only being used in Question 1;
other questions will introduce other assumptions.
Throughout the exam, assume we have already run the necessary import statements.
Consider the variable summed, defined below.
summed = hotels.groupby("Chain")["Number of Rooms"].sum().idxmax()
What is type(summed)?
int
str
Series
DataFrame
DataFrameGroupBy
Answer: str
When we do a groupby on the Chain column in
hotels, this means that the values in the
Chain column will be the indices of the DataFrame or Series
we get as output, in this case the Series
hotels.groupby("Chain")["Number of Rooms"].sum().
Since the values of Chain are strings, and since
.idxmax() will return a value from the index of the
aforementioned Series, summed is a string.
The average score on this problem was 88%.
In one sentence, explain what the value of summed means.
Phrase your explanation as if you had to give it to someone who is not a
data science major; that is, don’t say something like “it is the result
of grouping hotels by "Chain", selecting the
"Number of Rooms" column, …”, but instead, give the value
context.
Answer: summed is the name of the hotel
chain with the most total rooms
The result of the .groupby() and .sum() is
a Series indexed by the unique Chains, whose values are the
total number of rooms in hotels owned by each chain. The
idxmax() function gets the index corresponding to the
largest value in the Series, which will be the hotel chain name with the
most total rooms.
The average score on this problem was 97%.
Consider the variable curious, defined below.
curious = frame["Chain"].value_counts().idxmax()
Fill in the blank: curious is guaranteed to be equal to
summed only if frame has one row for every
____ in San Diego.
hotel
hotel chain
hotel room
neighborhood
Answer: hotel room
curious gets the most common value of Chain
in the DataFrame frame. We already know that
summed is the hotel chain with the most rooms in San Diego,
so curious only equals summed if the most
common Chain in frame is the hotel chain with
the most total rooms; this occurs when each row of frame is
a single hotel room.
The average score on this problem was 80%.
Fill in the blanks so that popular_areas is an array of
the names of the unique neighborhoods that have at least 5 hotels and at
least 1000 hotel rooms.
f = lambda df: __(i)__
popular_areas = hotels.groupby(__(ii)__).__(iii)__.__(iv)__What goes in blank (i)?
What goes in blank (ii)?
"Hotel Name"
"Location"
"Chain"
"Number of Rooms"
agg(f)
filter(f)
transform(f)
Answers:
df.shape[0] >= 5 and df["Number of Rooms"].sum() >= 1000"Location"filter(f)["Location"].unique() or equivalentWe’d like to only consider certain neighborhoods according to group
characteristics (having >= 5 hotels and >= 1000 hotel rooms), and
.filter() allows us to do that by excluding groups not
meeting those criteria. So, we can write a function that evaluates those
criteria on one group at a time (the df of input to
f is the subset of hotels containing just one
Location value), and calling filter(f) means
that the only remaining rows are hotels in neighborhoods that match
those criteria. Finally, all we have to do is get the unique
neighborhoods from this DataFrame, which are the neighborhoods for which
f returned True.
The average score on this problem was 83%.
Consider the code below.
cond1 = hotels["Chain"] == "Marriott"
cond2 = hotels["Location"] == "Coronado"
combined = hotels[cond1].merge(hotels[cond2], on="Hotel Name", how=???)??? with "inner" in the code
above, which of the following will be equal to
combined.shape[0]? min(cond1.sum(), cond2.sum())
(cond1 & cond2).sum()
cond1.sum() + cond2.sum()
cond1.sum() + cond2.sum() - (cond1 & cond2).sum()
cond1.sum() + (cond1 & cond2).sum()
??? with "outer" in the code
above, which of the following will be equal to
combined.shape[0]? min(cond1.sum(), cond2.sum())
(cond1 & cond2).sum()
cond1.sum() + cond2.sum()
cond1.sum() + cond2.sum() - (cond1 & cond2).sum()
cond1.sum() + (cond1 & cond2).sum()
Answers:
(cond1 & cond2).sum()cond1.sum() + cond2.sum() - (cond1 & cond2).sum()Note that cond1 and cond2 are boolean
Series, and hotels[cond1] and hotels[cond2]
are the subsets of hotels where
Chain == "Marriott and
"Location" == "Coronado", respectively.
When we perform an inner merge, we’re selecting every row where a
Hotel Name appears in both
hotels[cond1] and hotels[cond2]. This is the
same set of indices (and therefore hotel names, since those are unique)
as where (cond1 & cond2) == True. So, the length of
combined will be the same as the number of
Trues in (cond1 & cond2).
When we perform an outer merge, we’re selecting every row that
appears in either DataFrame, although there will not be repeats
for hotels that are both Marriott properties and are in Coronado. So, to
find the total number of rows in either DataFrame, we take the sum of
the sizes of each, and subtract rows that appear in both, which
corresponds to answer
cond1.sum() + cond2.sum() - (cond1 & cond2).sum().
The average score on this problem was 79%.
At the Estancia La Jolla, the hotel manager enters information about
each reservation in the DataFrame guests, after guests
check into their rooms. Specifically, guests has the
columns:
"id" (str): The booking ID
(e.g. "SN1459")."age" (int): The age of the primary occupant (the
person who made the reservation)."people" (int): The total number of occupants."is_business" (str): Whether or not the trip is a
business trip for the primary occupant (possible values:
"yes", "no", and
"partially")."company" (str): The company that the primary occupant
works for, if this is a business trip."loyalty" (int): The loyalty number of the primary
occupant. Note that most business travelers have a loyalty number.Some of the values in guests are missing.
What is the most likely missingness mechanism of the
"loyalty" column?
Missing by design
Missing at random
Not missing at random
Missing completely at random
Answer: missing at random
The description of loyalty indicates that most business
travelers have a loyalty number – in other words, that depending on the
value of is_business, the probability of a present value
for loyalty can increase or decrease. This is therefore an
example of MAR.
The average score on this problem was 67%.
What is the most likely missingness mechanism of the
"company" column?
Missing by design
Missing at random
Not missing at random
Missing completely at random
Answer: missing by design
The value of company is missing if the trip is a
business trip, and since this relationship should be deterministic, then
this column is missing by design.
The average score on this problem was 60%.
Fill in the blanks: To assess whether the missingness of
"is_business" depends on "age", we should
perform a __(i)__ with __(ii)__ as the test
statistic.
standard hypothesis test
permutation test
the total variation distance
the sample mean
the (absolute) difference in means
the K-S statistic
either the (absolute) difference in means or the K-S statistic, depending on the shapes of the observed distributions
Answers:
In part 1, we use a permutation test because we’re comparing two
sampled distributions (the values of age for rows with
missing vs. present values of is_business), rather than
comparing our sample distribution to a known population
distribution/metric.
For part 2, we should note that the test statistic, for each
iteration of our permutation test, is meant to compare two distributions
of the variable age, which is continuous. TVD is not
well-suited for this, since it compares discrete, categorical
distributions, and neither is “sample mean,” since we have two samples
to compare. Differences in means or the K-S statistic work because they
both compare two continuous distributions. However, there are cases in
which the difference in means might not capture differences in
distributions (for example, two distributions with the same mean but
very different standard deviation); this is the reason for the caveat in
the correct solution.
The average score on this problem was 68%.
Fill in the blanks: To assess whether the missingness of
"age" depends on "is business", we should
perform a __(i)__ with __(ii)__ as the test
statistic.
standard hypothesis test
permutation test
the total variation distance
the sample mean
the (absolute) difference in means
the K-S statistic
either the (absolute) difference in means or the K-S statistic, depending on the shapes of the observed distributions
Answers:
For part 1, the reasoning is the same as the previous part – the only difference is that now, we’re comparing two categorical distributions rather than two continuous ones.
In part 2, we can note that we’re now comparing the categorical
distributions of is_business, which can only have values of
"yes", "no", and "partially", for
rows with missing vs. present values of age. (Even though
age is continuous, since we’re only using whether or not
age is missing and not the actual values in the column,
this doesn’t really matter.) The only test statistic listed that is
meant to compare two categorical distributions is TVD, so this is the
correct solution.
The average score on this problem was 72%.
After running the code below, p is equal to the
simulated p-value for a statistical test.
obs = guests.groupby("is_business")["age"].median().loc["no"]
p = 0
for _ in range(10000):
s = guests.sample((guests["is_business"] == "no").sum(),
replace=False)
sm = s["age"].median()
p += (obs >= sm) / 10000standard hypothesis test
permutation test
Fill in the blanks: The alternative hypothesis being tested above is
that the median age of primary occupants not on a
business trip is __(ii)__ the median age of
__(iii)__.
greater than or equal to
greater than
equal to
not equal to
less than or equal to
less than
all primary occupants
primary occupants at least partially on a business trip (that is,
primary occupants who have an "is_business" value of
"yes" or "partially")
Answers:
For part 1, this is a standard hypothesis test, because instead of
shuffling the values of a particular column, we are sampling entire rows
of the DataFrame; the size of these samples is the same as the number of
guests who are not (even partially) on business trips. By sampling
randomly from the entire DataFrame, this assumes the null hypothesis
that the distribution of age of primary occupants not on a
business trip is equal to the distribution of age for occupants as a
whole. Therefore, this procedure is meant to simulate values of the
median age of a sample of size
guests["is_business"] == "no").sum(), and sampling random
rows means that we’re assuming that is_business == "no" and
age are unrelated.
For part 2, the samples capture how likely the deviation of the
observed statistic is to happen under the null hypothesis, but the
p-value is being calculated by adding up whenever the observed statistic
is greater or equal to the sample. This indicates that we’re doing a
one-tailed test, and since to reject the null hypothesis and provide
some evidence towards the alternate hypothesis, the p-value should be
lower, the alternate hypothesis should be the complement of
obs >= sm.
For part 3, the answer is “all primary occupants” because our
sampling procedure doesn’t sample just from (full or partial) business
travelers, but from the entire DataFrame. (In the line where we sample,
the only arguments are the number of rows we’re sampling, and that we’re
doing so without replacement – nothing about restricting which rows in
guest to sample.) In other words, we’re not comparing
primary occupants not on business trips to those on business trips, but
rather we’re comparing primary occupants to the entire dataset of
occupants.
The average score on this problem was 58%.
Weiyue proposes the following imputation scheme.
def impute(s):
return s.fillna(np.random.choice(s[s.notna()]))True or False: impute performs
probabilistic imputation, using the same definition of probabilistic
imputation we learned about in class.
True
False
Answer: False
In impute, np.random.choice will return a
single non-null value from s, and .fillna()
will fill every null value with this single value. Meanwhile,
probabilistic imputation draws a different value from a specified
distribution to fill each missing value, making it such that there won’t
be a single “spike” in the imputed distribution at a single chosen
value.
The average score on this problem was 41%.
Consider the following expressions and values.
>>> vals.isna().mean()
0.2
>>> vals.describe().loc[["min", "mean", "max"]]
min 2.0
mean 4.0
max 7.0
dtype: float64Given the above, what is the maximum possible value
of impute(vals).mean()? Give your answer as a number
rounded to one decimal place.
Answer: 4.6
The maximum possible value of impute(vals).mean() would
occur when every single missing value in vals is filled in
with the highest possible non-null value in vals. (As
discussed in the previous solution, impute selects only one
value from s to fill into every missing space.)
If this occurs, then the mean of the imputed Series will be weighted mean of the available data and the filled data, and given the numbers in the question, this is 0.8 \cdot 4 + 0.2 \cdot 7, or 4.6.
The average score on this problem was 50%.
Which of the following statements below will always evaluate to
True?
vals.std() < impute(vals).std()
vals.std() <= impute(vals).std()
vals.std() == impute(vals).std()
vals.std() >= impute(vals).std()
vals.std() > impute(vals).std()
None of the above
Answer: None of the above
Since the value which impute() will choose to impute
with is random, the effect that it has on the standard deviation of
vals is unknown. If the missing values are filled with a
value close to the mean, this could reduce standard deviation; if they
are filled with a value far from the mean, this could increase standard
deviation. (Of course, the imputation will also shift the mean, so
without knowing details of the Series, it’s impossible to come up with
thresholds.) In any case, since the value for imputation is chosen at
random, none of these statements will always be true, and so
the correct answer is “none of the above.”
The average score on this problem was 38%.
Suppose site is a BeautifulSoup object
instantiated on the HTML document below.
<html>
<div align="center">
<h3>Luxury Hotels in Bali from May 2-6, 2024 for Ethan</h3>
<div class="chain" name="Hilton">
<h3 style="color: blue">Hilton Properties in Bali</h3>
</div>
<div class="chain" name="Marriott">
<h3 style="color: red">Marriott Properties in Bali</h3>
</div>
<div __(i)__>
__(ii)__
</div>
</div>
</html>What does len(site.find_all("div")) evaluate to? Give
your answer as an integer. For this part only, assume that both blank
(i) and blank (ii) are left blank.
Answer: 4
The answer simply requires counting the number of div
elements, making sure not to double-count opening and closing tags.
The average score on this problem was 82%.
Fill in the blank so that chain_color takes in the name
of a hotel chain and returns the color used to display the hotel chain
in site. For example, chain_color("Hilton") should return
"blue" and chain_color("Marriott") should
return "red".
chain_color = lambda chain: site.____.split()[-1]Answer:
find("div", attrs={"name": chain}).find("h3").get("style")
The solution finds all div elements whose
name attribute is equal to the function input
chain (which is how the chains are defined in the HTML
document). Then, the colors are stored as part of the style
attribute in an h3 tag within that div, so we
find the first – and in this document, only – h3 tag within
the div and get its style attribute. This
returns a string like color: red, from which the given code
.split()[-1] returns the last word, which is the correct
color.
The average score on this problem was 67%.
Fill in blanks (i) and (ii) in site so that the
following all evaluate to True:
len(site.find_all("div", class_ ="chain")) == 2chain_color("Hyatt") == "purple"site.find_all("div")[-1].text == ""Answers:
name = "Hyatt"<h3 style="color: purple"></h3>In order to make all of the three given statements true, we need to
make it such that there are 2 div elements with class
chain, the chain_color function returns
purple for Hyatt, and the last
div tag in the document has no text.
We do this by defining a div similar to the previous
two, but without the chain class (because there are already
2 in the document). In order for chain_color("Hyatt") to
return purple, we add "Hyatt" as a
name attribute in the div, and add an
h3 tag within that div with
style="color: purple". However, since the last statement
requires the last div in the document has no text, and the
div we’re currently making will be the final one, we don’t
include any text in the h3 tag. (Note that because the
chain_color function doesn’t use the hotel name in the text
to find a given chain’s name, but rather the name attribute in the
enclosing div tag.)
The average score on this problem was 90%.
Dylan finds a messy text file containing room availability and pricing information at his favorite local hotel, the Manchester Grand Hyatt.
Availability strings are formatted like so:
avail = """Standard: Available, This23: Available,
Suite: Available, Economy: Not Available,
Rooms are Available, Deluxe: Available"""Fill in the blank below so that exp1 is a regular
expression such that if s is an availability string in the
format above, re.findall(exp1, s) will return a list of all
of the available room categories in s. Example behavior is
given below.
>>> re.findall(exp1, avail)
["Standard", "Suite", "Deluxe"] # Categories don't include numbersNote that your answer needs to work on other availability strings;
you should not hard-code "Standard", "Suite",
or "Deluxe".
exp1 = r"_____________"Answer: ([A-Za-z]+): Available
In the above availability strings, we’re looking for a one-or-more-length sequence of letters (not numbers, as mentioned in the problem), followed by a colon and the word “Available.” However, since we only want to return the room type, and not the colon or the word “Available,” we use a capturing group (the parentheses) to just return the word before the colon.
The average score on this problem was 57%.
Consider the string prices, defined below.
one = "Standard room: $120, $2.Deluxe room: $200.75"
two = "Other: 402.99, Suite: $350.25"
prices = one + ", " + twore.findall(r"\$\d+\.\d{2}$", prices) evaluate
to? ["$200.75", "$402.99", "$350.25"]
["200.75", "402.99", "350.25"]
["$120", "$200.75", "$350.25"]
["$350.25"]
["$200.75", "$350.25"]
re.findall(r"\$?(\d+\.\d{2})", prices)
evaluate to? ["$200.75", "$402.99", "$350.25"]
["200.75", "402.99", "350.25"]
["$120", "$200.75", "$350.25"]
["$350.25"]
["$200.75", "$350.25"]
Answers:
["$350.25"]["200.75", "402.99", "350.25"]In the first part, the string that the pattern matches is a dollar
sign ($), one or more digits (\d+), a period
(\.), two digits (\d{2}), followed by the end
of the string ($). Since the string we’re passing into
re.findall is prices, which is the
concatenation of one + ", " + two, the only option that
matches is the last price displayed, "$350.25". (If we had
not specified the match ending with the end of the string,
"$200.75" would also have been a match.)
In the second part, the beginning of the pattern is
"\$?", which means to match zero or one instance
of the dollar sign character. In most cases, this means that if there is
a dollar sign before the remainder of the pattern, it will be included
in the match, but if not, the rest of the pattern will still match.
However, the capturing group around the remainder of the pattern means
that in either case, only the remainder of the pattern after the dollar
sign is captured. (So, in this particular example, the \$?
has no effect on the output.)
The rest of the pattern is structured similarly to the previous part, except now, the pattern does not require the end of the string after the price, so we’re just selecting sequences of digits followed by a period and two more digits, which is how we get our solution.
The average score on this problem was 65%.
Gabriel decides to look at reviews for the Catamaran Resort Hotel and Spa. TripAdvisor has 96 reviews for the hotel; of those 96, Gabriel’s favorite review was:
"close to the beach but far from the beach beach"What is the TF of "beach" in Gabriel’s favorite review?
Give your answer as a simplified fraction.
Answer: \frac{3}{10}
The answer is simply the proportion of words in the sentence that are
the word "beach". There are 10 words in the sentence, 3 of
which are "beach".
The average score on this problem was 97%.
The TF-IDF of "beach" in Gabriel’s favorite review is
\frac{9}{10}, when using a base-2
logarithm to compute the IDF. How many of the reviews on TripAdvisor for
this hotel contain the term "beach"?
3
6
8
12
16
24
32
Answer: 12
The TF-IDF is the product of the TF and IDF terms. So if the TF-IDF
of this document is \frac{9}{10}, and
the TF is \frac{3}{10}, as established
in the last part, the IDF of the term "beach" is 3. The IDF
for a word is the log of the inverse of the proportion of documents in
which the word appears. So, since we know there are 96 total
documents.
3 = log_{2}(\frac{96}{\text{\# documents containing "beach"}})
2^{3} = \frac{96}{\text{\# documents containing "beach"}}
\boxed{12} = {\text{\# documents containing "beach"}}
The average score on this problem was 76%.
Tiffany decides to look at reviews for the same hotel, but she
modifies them so that the only terms they contain are
"taco" and "sand". The bag-of-words
representations of three reviews are shown as vectors below.
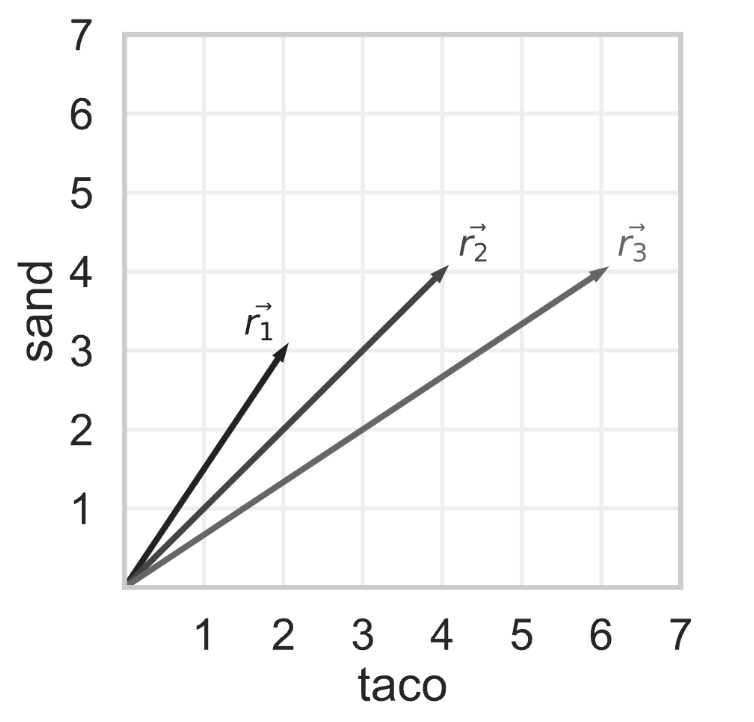
Using cosine similarity to measure similarity, which pair of reviews are the most similar? If there are multiple pairs of reviews that are most similar, select them all.
\vec{r}_1 and \vec{r}_2
\vec{r}_1 and \vec{r}_3
\vec{r}_2 and \vec{r}_3
Answer: \vec{r}_1 and \vec{r}_2, and \vec{r}_2 and \vec{r}_3
The cosine similarity of two vectors \vec{a} and \vec{b} is \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \cdot ||\vec{b}||}.
The cosine similarity of \vec{r}_1 and \vec{r}_2 is:
\frac{2 \cdot 4 + 3 \cdot 4}{\sqrt{13} \cdot \sqrt{32}} = \frac{20}{4 \cdot \sqrt{26}} = \frac{5}{\sqrt{26}}
The cosine similarity of \vec{r}_1 and \vec{r}_3 is:
\frac{2 \cdot 6 + 3 \cdot 4}{\sqrt{13} \cdot \sqrt{52}} = \frac{24}{26} = \frac{12}{13}
The cosine similarity of \vec{r}_2 and \vec{r}_3 is:
\frac{4 \cdot 6 + 4 \cdot 4}{\sqrt{32} \cdot \sqrt{52}} = \frac{40}{8 \cdot \sqrt{26}} = \frac{5}{\sqrt{26}}
\frac{12}{13} \approx 0.9231, and \frac{5}{\sqrt{26}} \approx 0.9806, so our answer is vector pairs \vec{r}_1 and \vec{r}_2, and \vec{r}_2 and \vec{r}_3
The average score on this problem was 74%.
Consider the corpus of length 13 below, made up of 6 As, 4 Bs, 1 C, and 2 Rs (and no other tokens). Here, each individual character is treated as its own token.
\text{ABABRACABABRA}
Let P be a function that computes the probability of the input sequence using a bigram model trained on the above corpus. For example, P(BR) is the probability of the sequence BR, using a bigram language model trained on the above corpus.
What is P(ABRA)? Give your answer as a simplified fraction.
Answer: \frac{12}{65}
Using a bigram model, we find the probability of the first token, then for each remaining token, find its probability given just the previous token. The probability P(\text{X} | \text{Y}) is simply the proportion of times that token X is the next token after the previous token Y. So, for this corpus and input sequence, we have:
P(\text{A}) = \frac{6}{13}
P(\text{B} | \text{A}) = \frac{4}{5}
P(\text{R} | \text{B}) = \frac{2}{4} = \frac{1}{2}
P(\text{A} | \text{R}) = \frac{2}{2} = 1
So, we just have to multiply these probabilities together, and we get \frac{12}{65}.
Note that the denominator for P(\text{B} | \text{A}) is 5, not 6, even though there are 6 occurrences of the letter A. This is because the final one occurs at the end of the sentence, and we’re not using a stop token or anything else designating the end of the sequence. So there are only 5 instances of “A” where we have a subsequent token, which is how we make our probability model.
The average score on this problem was 47%.
Suppose n is a positive integer. Let [AB]^{n} be the result of repeating the sequence AB n times. For example, [AB]^{4} is ABABABAB and [AB]^{5} is ABABABABAB.
Then, it is always the case that:
P([AB]^{n}) = 2p (\frac{c}{d})^{k}
where:
2
\frac{n}{2} - 1
\frac{n}{2}
n - 1
n
n + 1
Hint: Start by finding P(AB), P(ABAB), and P(ABABAB).
Answer:
From our work on the previous question, we can see that 2p is equal to P(\text{A}) \cdot P(\text{B} | \text{A}), or in other words, the probability of the sequence AB.
The probability of sequence ABAB will be the probability of sequence AB, times P(\text{A} | \text{B}) \cdot P(\text{B} | \text{A}). More generally, we can see that after the first pair of tokens AB (which has a different probability since the first token is the first in the sequence, and therefore isn’t conditioned on B), each repetition of AB multiplies a probability of P(\text{A} | \text{B}) \cdot P(\text{B} | \text{A}).
Therefore, our resulting fraction \frac{c}{d} is simply this probability P(\text{A} | \text{B}) \cdot P(\text{B} | \text{A}). P(\text{A} | \text{B}) is \frac{1}{2}, and we already found that P(\text{B} | \text{A}) is \frac{4}{5}, so the resulting fraction is \frac{2}{5}. So c = 2, and d = 5.
This fraction is multiplied once for each repetition of AB after the first one (which has a different probability, represented by 2p), and so the exponent should be n-1.
The average score on this problem was 66%.
Suppose Yutian builds a classifier that predicts whether or not a hotel provides free parking. The confusion matrix for her classifier, when evaluated on our training set, is given below.

What is the precision of Yutian’s classifier? Give your answer as a simplified fraction.
Answer: \frac{8}{13}
Precision is the proportion of predicted positives that actually were positives. So, given this confusion matrix, that value is \frac{8}{8 + 5}, or \frac{8}{13}.
The average score on this problem was 89%.
Fill in the blanks: In order for Yutian’s classifier’s recall to be
equal to its precision, __(i)__ must be equal to
__(ii)__.
A
B
2
3
4
5
6
8
13
14
20
40
50
80
Answer:
We already know that the precision is \frac{8}{13}. Recall is the proportion of true positives that were indeed classified positives, which in this matrix is \frac{8}{B + 8}. So, in order for precision to equal recall, B must be 5.
The average score on this problem was 96%.
Now, suppose both A and B are unknown. Fill in the blanks: In order
for Yutian’s classifier’s recall to be equal to its accuracy,
__(i)__ must be equal to __(ii)__.
A + B
A - B
B - A
A \cdot B
\frac{A}{B}
\frac{B}{A}
2
3
4
5
6
8
13
14
20
40
50
80
Hint: To verify your answer, pick an arbitrary value of A, like A = 10, and solve for the B that sets the model’s recall equal to its accuracy. Do the specific A and B you find satisfy your answer above?
Answer:
We can solve this problem by simply stating recall and accuracy in terms of the values in the confusion matrix. As we already found, recall is \frac{8}{B+8}. Accuracy is the sum of correct predictions over total number of predictions, or \frac{A + 8}{A + B + 13}. Then, we simply set these equal to each other, and solve.
\frac{8}{B+8} = \frac{A + 8}{A + B + 13} 8(A + B + 13) = (A + 8)(B + 8) 8A + 8B + 104 = AB + 8A + 8B + 64 104 = AB + 64 AB = 40
The average score on this problem was 79%.
Harshi is trying to build a decision tree that predicts whether or not a hotel has a swimming pool.
Suppose + represents the “has pool” class and \circ represents the “no pool” class. One of the nodes in Harshi’s decision tree has 12 points, with the following distribution of classes.
++++\circ\circ\circ\circ\circ\circ\circ\,\circ
Consider the following three splits of the node above.
Split 1:
Split 2:
Split 3:
Which of the six nodes above have the same entropy as the original node? Select all that apply.
Split 1’s “Yes” node
Split 1’s “No” node
Split 2’s “Yes” node
Split 2’s “No” node
Split 3’s “Yes” node
Split 3’s “No” node
Answer: Split 1’s “Yes” node, Split 1’s “No” node, and Split 2’s “No” node
The definition of entropy for a node is:
\text{entropy} = - \sum_C p_C \log_2 p_C
where C is each label class, and p_C is the proportion of points in the node in class C.
We can note that in binary classification, two nodes will have the same entropy if they have the same relative distribution of classes, or if the distributions of classes are complements of each other. (For example, a node with 75% positives and 25% negatives has the same entropy as a node with 25% positives and 75% negatives.) So, in this problem, we need only find nodes with the same proportions as the original node, which has 4 positives (\frac{1}{3}) and 8 negatives (\frac{2}{3}).
The average score on this problem was 88%.
Which of the six nodes above have the lowest entropy? If there are multiple correct answers, select them all.
Split 1’s “Yes” node
Split 1’s “No” node
Split 2’s “Yes” node
Split 2’s “No” node
Split 3’s “Yes” node
Split 3’s “No” node
Answer: Split 3’s “Yes” node
The lowest possible entropy for a distribution occurs when it takes on only one value. In the definition of entropy, \log_2 p_C will be 0 when p_C is 1, so entropy will be zero when all points are of the same class. This only occurs in one of the given nodes, Split 3’s “Yes” node.
The average score on this problem was 93%.
Jasmine and Aritra are trying to build models that predict the number
of open rooms a hotel room has. To do so, they use price,
the average listing price of rooms at the hotel, along with a one hot
encoded version of the hotel’s chain. For the
purposes of this question, assume the only possible hotel chains are
Marriott, Hilton, and Other.
First, Jasmine fits a linear model without an intercept term. Her prediction rule, H_1, looks like:
H_{1}(x) = w_1 \cdot \texttt{price} + w_2 \cdot \texttt{is\_Marriott} + w_3 \cdot \texttt{is\_Hilton} + w_4 \cdot \texttt{is\_Other}
After fitting her model, \vec{w}^* = \begin{bmatrix}−0.5 \\ 200 \\ 300 \\ 50 \end{bmatrix}.
Answers:
If we plug in the weights from \vec{w}^* into the equation for H_1(x), noting that the values of the one-hot variables are either 0 or 1, we get -0.5 \cdot 250 + 200 \cdot 1 + 300 \cdot 0 + 50 \cdot 0, or -125 + 200, or 75.
For part 2, the difference between predicted and actual number of rooms is 75 - 45 = 30, and the squared loss is simply 30^2 = 900.
For part 3, the answer is False, since the fact that our best-fit line has an error at a given input does not mean that this input was not seen in the training data. In other words, the line of best fit does not always have to pass through all of the training points (and due to overfitting, in most cases you don’t want it to).
The average score on this problem was 87%.
Then, on the same training set, Aritra fits a linear model,
with an intercept term but without the is_Other
feature. His new prediction rule, H_2,
now looks like:
H_2(x) = \beta_0 + \beta_1 \cdot \texttt{price} + \beta_2 \cdot \texttt{is\_Marriott} + \beta_3 \cdot \texttt{is\_Hilton}
After fitting his model, Aritra finds optimal coefficients \beta_{0}^{*}, \beta_{1}^{*}, \beta_{2}^{*}, and \beta_{3}^{*}.
True
False
True
False
Answers:
In model H_1, there is redundant
information in the one-hot encoded features, creating multicollinearity.
The second model H_2 removes the
is_Other feature, but the intercept term it is replaced
with serves a similar function. When is_Other is true, the
prediction of H_1 is w_1 \cdot \texttt{price} + w_4, and the
prediction of H_2 is \beta_1 \cdot \texttt{price} + \beta_0. The
multicollinearity in H_1 doesn’t affect
model performance relative to model 2, but it will yield different
parameter estimates since there will be multiple solutions, unlike with
H_2. However, the models will have
equivalent best solutions, even if the parameters differ, so both parts
are True.
The average score on this problem was 53%.
As a reminder,
H_{1}(x) = w_1 \cdot \texttt{price} + w_2 \cdot \texttt{is\_Marriott} + w_3 \cdot \texttt{is\_Hilton} + w_4 \cdot \texttt{is\_Other}
\vec{w}^* = \begin{bmatrix}−0.5 \\ 200 \\ 300 \\ 50 \end{bmatrix}
H_2(x) = \beta_0 + \beta_1 \cdot \texttt{price} + \beta_2 \cdot \texttt{is\_Marriott} + \beta_3 \cdot \texttt{is\_Hilton}
After fitting his model, Aritra finds \beta_{0}^{*} = 50. Given that, what are \beta_{1}^{*}, \beta_{2}^{*}, and \beta_{3}^{*}? Give your answers as numbers with no variables.
Answers:
As we saw in the previous question, these models should yield an
equivalent best-fit line. The relationship between price
and predicted outcome will be the same, so \beta_{1}^{*} will be -0.5, the same weight as in H_1.
If \beta_{0}^{*} = 50, this means we
are adding 50 to all predictions, and that the “adjustments” we make to
the prediction for is_Marriott and is_Hilton
should therefore be reduced to compensate for this; therefore, the new
weights \beta_{2}^{*} and \beta_{3}^{*} will be 150 and 250.
The average score on this problem was 69%.
Diego also wants to build a model that predicts the number of open rooms a hotel has, given various other features. He has a training set with 1200 rows available to him for the purposes of training his model.
Diego fits a regression model using the GPTRegression
class. GPTRegression models have several hyperparameters
that can be tuned, including context_length and
sentience.
To choose between 5 possible values of the hyperparameter
context_length, Diego performs k-fold cross-validation.
GPTRegression model fit?4k
5k
240k
6000k
4(k − 1)
5(k − 1)
240(k − 1)
6000(k − 1)
GPTRegression model is fit,
it appends the number of points in its training set to the list
sizes. Note that after performing cross- validation,
len(sizes) is equal to your answer to the previous
subpart.What is sum(sizes)?
4k
5k
240k
6000k
4(k − 1)
5(k − 1)
240(k − 1)
6000(k − 1)
Answers:
When we do k-fold cross-validation for one single hyperparameter value, we split the dataset into k folds, and in each iteration i, train the model on the remaining k-1 folds and evaluate on fold i. Since every fold is left out and evaluated on once, the model is fit in total k times. We do this once for every hyperparameter value we want to test, so the total number of model fits required is 5k.
In part 2, we can note that each model fit is performed on the same size of data – the size of the remaining k-1 folds when we hold out a single fold. This size is 1 - \frac{1}{k} = \frac{k-1}{k} times the size of the entire dataset, in this case, 1200 \cdot \frac{k-1}{k}, and we fit a model on a dataset of this size 5k times. So, the sum of the training sizes for each model fit is:
5k \cdot \frac{k-1}{k} \cdot 1200 = 6000(k-1)
The average score on this problem was 66%.
The average training error and validation error for all 5 candidate
values of context_length are given below.
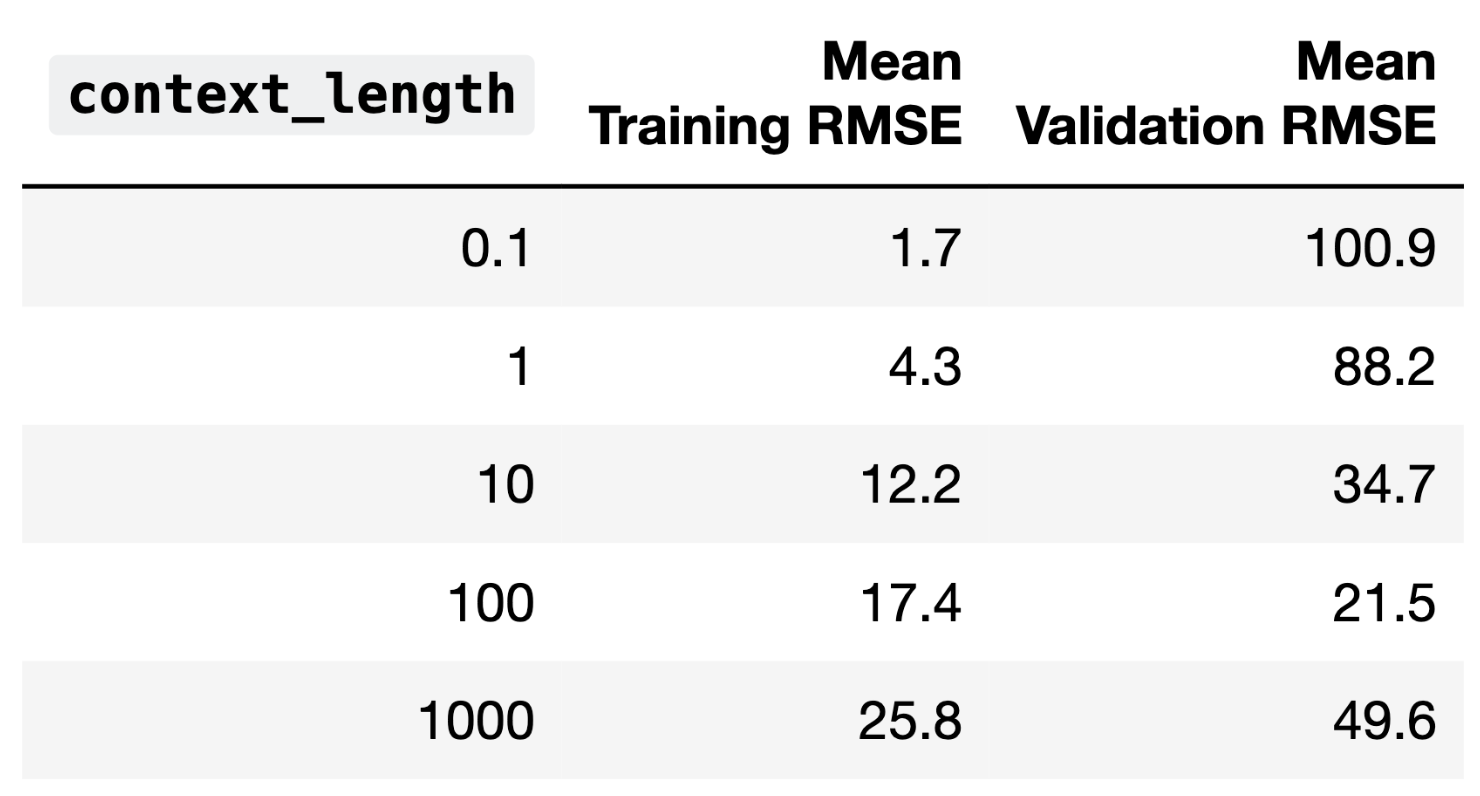
Fill in the blanks: As context_length increases, model
complexity __(i)__. The optimal choice of
context_length is __(ii)__; if we choose a
context_length any higher than that, our model will
__(iii)__.
increases
decreases
0.1
1
10
100
1000
overfit the training data and have high bias
underfit the training data and have high bias
overfit the training data and have low bias
underfit the training data and have low bias
Answers:
In part 1, we can see that as context_length increases,
the training error increases, and the model performs worse. In general,
higher model complexity leads to better model performance, so here,
increasing context_length is reducing model
complexity.
In part 2, we will choose a context_length of 100, since
this parameterization leads to the best validation performance. If we
increase context_length further, the validation error
increases.
In part 3, since increased context_length indicates
less complexity and worse training performance, increasing the
context_length further would lead to underfitting, as the
model would lack the expressiveness or number of parameters required to
capture the data. Since training error represents model bias, and since
high variance is associated with overfitting, a further
increase in context_length would mean a more biased
model.
The average score on this problem was 65%.