Spring 2024 Final Exam

← return to practice.dsc80.com

Instructor(s): Sam Lau

This exam was administered in-person. The exam was closed-notes, except students were allowed to bring two two-sided cheat sheets. No calculators were allowed. Students had 180 minutes to take this exam.

The Open e-commerce dataset contains data about people’s Amazon.com purchases. To collect the data, the researchers asked participants to fill out a survey. Only participants who completed the survey were recorded in the data. In one part of the survey, participants were given instructions to download their Amazon purchase history and share it with the researchers. Since this step was not required, not all participants shared their Amazon purchase history with the researchers. The dataset contains two tables, df and survey. The df table was created from participants’ purchase history and records individual items purchased from Amazon.

Problem 1

Fill in Python code below so that the last line of each code snippet evaluates to each desired result, using the df and survey DataFrames described on Page 1 of the Reference Sheet. You may not use for or while loops in any answer for this question. For convenience, the first few rows of df (top) and survey (bottom) are displayed below.


Problem 1.1

Find the participant ID of the person who made the most recent purchase in the dataset.

df.sort_values(__(a)__, ascending=True).iloc[__(c)__, __(b)__]

Answer:

(a): date

(b): -1

(c): -1



Problem 1.2

Create a DataFrame that compares the range of item costs for people with diabetes and people that don’t have diabetes. The DataFrame should be indexed by the unique values in the diabetes column (Yes and No) and have one column: the range of item costs (max cost - min cost) for each group.

def f(x):
    return __(a)__

(df.merge(survey, on='id')
   .groupby(__(b)__)[__(c)__]
   .__(d)__(f))

Answer:

(a): x.max() - x.min()

(b): 'diabetes'

(c): 'cost'

(d): agg


Problem 2


Problem 2.1

What is the most likely missingness mechanism for the state column in df?

Answer: Missing by design



Problem 2.2

What is the most likely missingness mechanism for the income column in survey?

Answer: Missing at random


Problem 3

The code snippet below uses a for loop.

mystery = 0
for i in df['id'].unique():
    temp = df[df['id'] == i]
    if temp['q'].sum() > 100:
        mystery += 1


Problem 3.1

Rewrite the snippet without using any loops.

mystery = (df.groupby(__(a)__)
           .__(b)__(lambda x: __(c)__)
           [__(d)__].__(e)__())

Answer:

(a): 'id'

(b): filter

(c): x['q'].sum() > 100

(d): 'id'

(e): nunique



Problem 3.2

Suppose you see the output below:

>>> df['id'].value_counts()
P2955    200
P3001    150
P3125    100
Name: id, Length: 3, dtype: int64

Fill in the blank in the sentence below with a single number.

The code without for loops runs approximately _______ times faster than the code with a for loop.

Answer: 3


Problem 4

You want to use regular expressions to extract out the number of ounces from the 5 product names below.

Index Product Name Expected Output
0 Adult Dog Food 18-Count, 3.5 oz Pouches 3.5
1 Gardetto’s Snack Mix, 1.75 Ounce 1.75
2 Colgate Whitening Toothpaste, 3 oz Tube 3
3 Adult Dog Food, 13.2 oz. Cans 24 Pack 13.2
4 Keratin Hair Spray 2!6 oz 6

The names are stored in a pandas Series called names. For each snippet below, select the indexes for all the product names that will not be matched correctly.


Problem 4.1

Snippet:

regex = r'([\d.]+) oz'
names.str.findall(regex)

Answer: 1



Problem 4.2

Snippet:

regex = r'(\d+?.\d+) oz|Ounce'
names.str.findall(regex)

Answer: 1, 2, 4


Problem 5

Suppose you define a DataFrame t as follows:

t = (survey.merge(df, on='id', suffixes=('', '2'))
     .assign(is_ca=t['state'] == 'California',
             is_boot=t['cat'] == 'BOOT',
             is_tool=t['cat'] == 'TOOLS'))

The first few rows of t are shown below:

For each pivot table below, state whether it is possible to observe Simpson’s paradox without any extra information about the data.


Problem 5.1

Pivot table:

t.pivot_table(
    index='is_ca',
    columns='is_boot',
    values='cost',
    aggfunc='count',
)

Answer: No



Problem 5.2

Pivot table:

t.pivot_table(
    index='is_ca',
    columns='is_tool',
    values='cost',
    aggfunc='mean',
)

Answer: Yes


Problem 6

For each hypothesis test below, select the one correct procedure to simulate a single sample under the null hypothesis, and select the one test statistic that can be used for the hypothesis test among the choices given.

For convenience, the first few rows of df (top) and survey (bottom) are displayed below; see your Reference Sheet for the full details.


Problem 6.1

Null: Every purchase is equally likely to happen in all 50 states.

Alternative: At least one state is more likely to have purchases than others.

Simulation procedure:

Test statistic:

Answer:

Simulation procedure: np.random.multinomial(len(df), [1/50] * 50)

Test statistic: Total variation distance



Problem 6.2

Null: The income distribution of people who smoke marijuana is the same as the income distribution for people who don’t smoke marijuana.

Alternative: The income distributions are different.

Simulation procedure:

Test statistic:

Answer:

Simulation procedure: np.random.permutation(survey['income'])

Test statistic: Total variation distance



Problem 6.3

Null: The distribution of prices for items with missing categories is the same as the distribution of prices for items with recorded categories.

Alternative: Items with missing categories are more expensive than items with with recorded categories.

Simulation procedure:

Test statistic:

Answer:

Simulation procedure: np.random.permutation(df['cost'])

Test statistic: Difference in means


Problem 7

Suppose that df doesn’t have any missing data in the cost column. Sam accidentally loses values from the cost column and values are more likely to be missing for states with expensive purchases. Sam’s data is stored in a DataFrame called missing.

To recover the missing values, Sam applies the imputation methods below to the cost column in missing, then recalculates the mean of the cost column. For each imputation method, choose whether the new mean will be lower (-), higher (+), exactly the same (=), or approximately the same (\approx) as the original mean of the cost column in df (the data without any missing observations).


Problem 7.1

missing['cost'].fillna(missing['cost'].mean())

Answer: -



Problem 7.2

def mystery(s):
    return s.fillna(s.mean())
missing.groupby('state')['cost'].transform(mystery).mean()

Answer: \approx



Problem 7.3

def mystery2(s):
    s = s.copy()
    n = s.isna().sum()
    fill_values = np.random.choice(s.dropna(), n)
    s[s.isna()] = fill_values
    return s

missing.groupby('state')['cost'].transform(mystery2).mean()

Answer: \approx


Problem 8

Suppose you are trying to scrape album names from a website. The website has an HTML table structured as follows:

<table><thead>
  <tr>
    <th>Name</th> <th>Price</th> <th>Number of Reviews</th>
  </tr></thead>
<tbody>
  <tr class="row">
    <td>Radical Optimism</td> <td>25</td> <td>10000</td>
  </tr>
  <tr class="row">
    <td>Hit Me Hard and Soft</td> <td>30</td> <td>12000</td>
  </tr>
  <tr class="row">
    <td>SOS</td> <td>18</td> <td>30000</td>
  </tr>
  <!-- 997 <tr> elements omitted -->
</tbody>
</table>

Notice that the <tbody> tag contains 1000 <tr> elements, but only the first three are shown above. Suppose that you’ve read the HTML table above into a BeautifulSoup object called soup. Fill in the code below so that the albums variable contains a list of all the album names with (strictly) more than 15,000 reviews.

albums = []
for tag in soup.find_all(___(a)___):
    reviews = int(___(b)___)
    if reviews > 15000:
        album = ___(c)___
        albums.append(album)


Problem 8.1

What should go in blank (a)?

Answer: class_="row"



Problem 8.2

What should go in blank (b)?

Answer: tag.find_all('td')[2].text



Problem 8.3

What should go in blank (c)?

Answer: tag.find('td').text


Problem 9

You create a table called gums that only contains the chewing gum purchases of df, then you create a bag-of-words matrix called bow from the name column of gums. The bow matrix is stored as a DataFrame shown below:

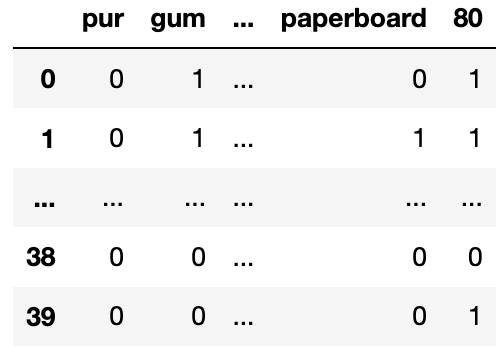
You also have the following outputs:

>>> bow_df.sum(axis=0)    >>> bow_df.sum(axis=1)    >>> bow_df[0, 'pur']
pur            5          0     21                  0
gum           41          1     22
sugar          2          2     22                  >>> (bow_df['paperboard'] > 0).sum()
              ..                ..                  20
90             4          37    22
paperboard    22          38    10                  >>> bow_df['gum'].sum()
80            20          39    17                  41
Length: 139               Length: 40

For each question below, write your answer as an unsimplified math expression (no need to simplify fractions or logarithms) in the space provided, or select “Need more information” if there is not enough information provided to answer the question.


Problem 9.1

What is the TF-IDF for the word pur in document 0?

Answer: 0



Problem 9.2

What is the TF-IDF for the word gum in document 0?

Answer: Need more information



Problem 9.3

What is the TF-IDF for the word paperboard in document 1?

Answer: \frac{1}{22} \log \left(\frac{40}{20} \right) = \frac{1}{22}


Problem 10

The two plots below show the total number of boots (top) and sandals (bottom) purchased per month in the df table. Assume that there is one data point per month.

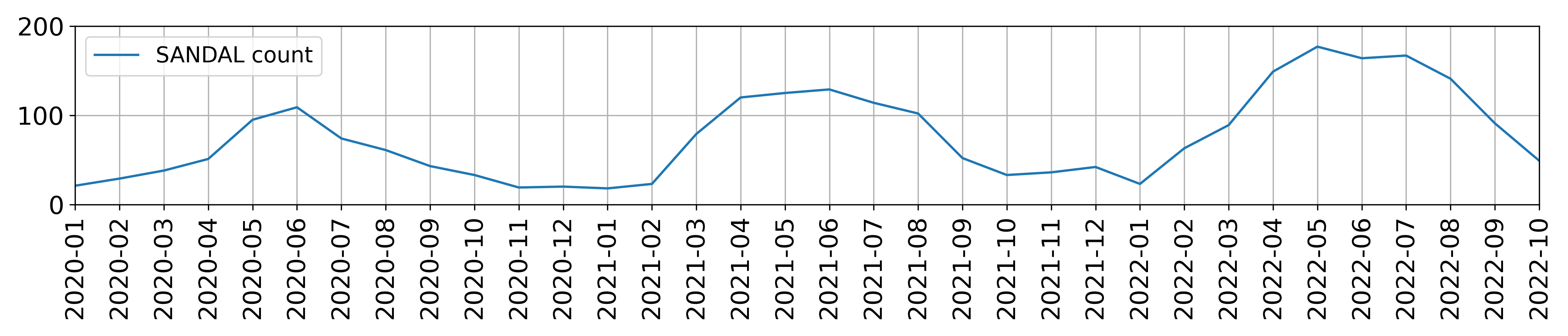
For each of the following regression models, use the visualizations shown above to select the value that is closest to the fitted model weights. If it is not possible to determine the model weight, select “Not enough info”. For the models below:


Problem 10.1

boot = w_0

w_0:

Answer: 50



Problem 10.2

boot = w_0 + w_1 \cdot \text{sandal}

w_0:

w_1:

Answer:

w_0: 100

w_1: -1



Problem 10.3

boot = w_0 + w_1 \cdot (\text{summer=1})

w_0:

w_1:

Answer:

w_0: 100

w_1: -80



Problem 10.4

sandal = w_0 + w_1 \cdot (\text{summer=1})

w_0:

w_1:

Answer:

w_0: 20

w_1: 80



Problem 10.5

sandal = w_0 + w_1 \cdot (\text{summer=1}) + w_2 \cdot (\text{winter=1})

w_0:

w_1:

w_2:

Answer:

w_0: Not enough info

w_1: Not enough info

w_2: Not enough info


Problem 11

Suppose you fit four different models to predict whether someone has an income greater than $100,000 a year using their purchase history. You split the data into a training and test set and use 3-fold cross-validation. The table below shows all the calculated accuracies for each model (higher accuracy is better).


Problem 11.1

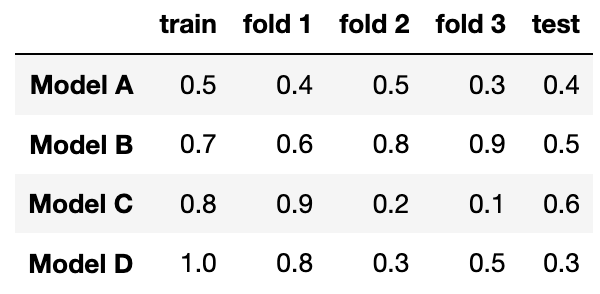
Which model has the lowest model bias?

Answer: Model D



Problem 11.2

Which model most severely underfits the data?

Answer: Model A



Problem 11.3

Which model most severely overfits the data?

Answer: Model D



Problem 11.4

Which model should you pick overall?

Answer: Model B


Problem 12

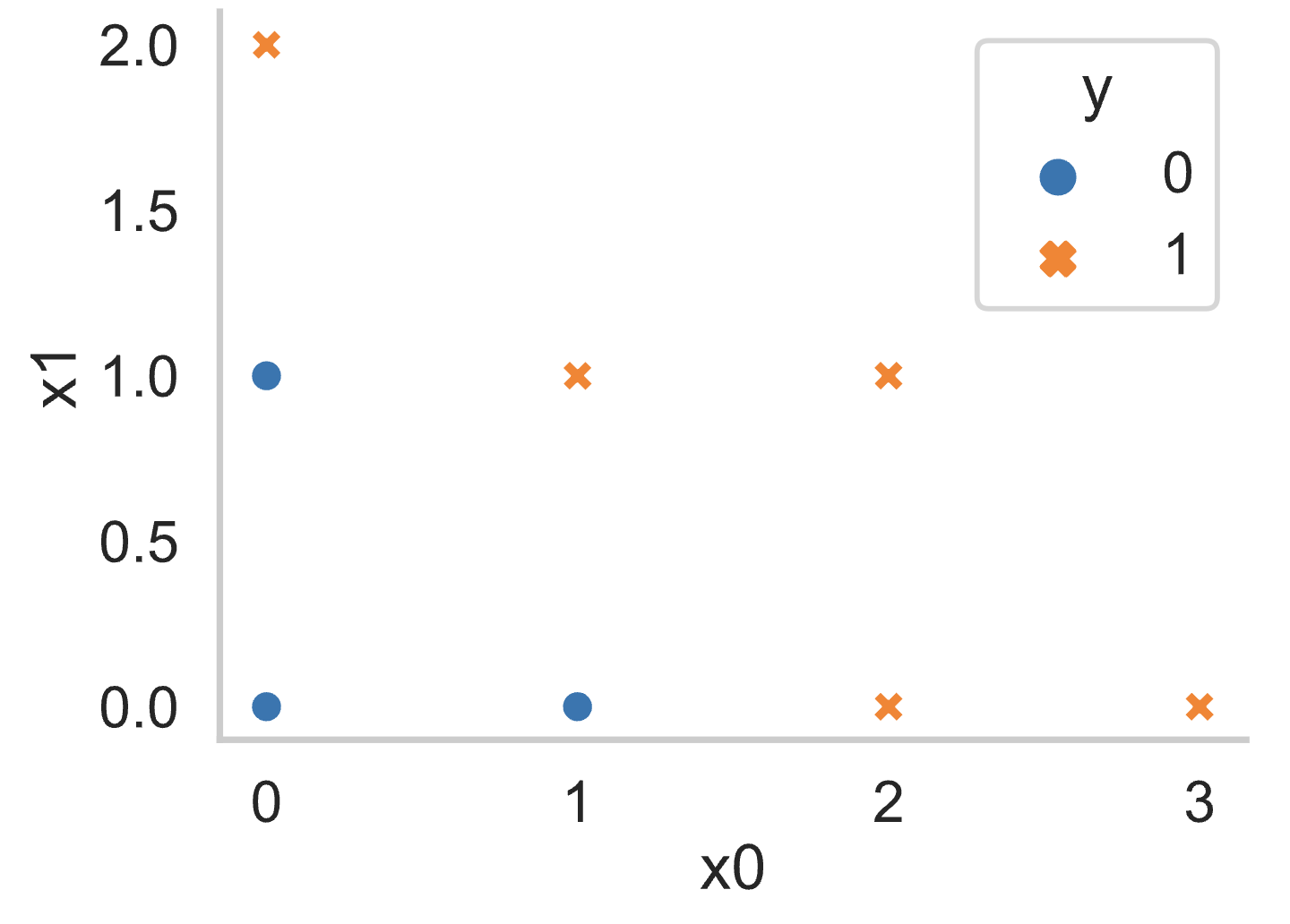
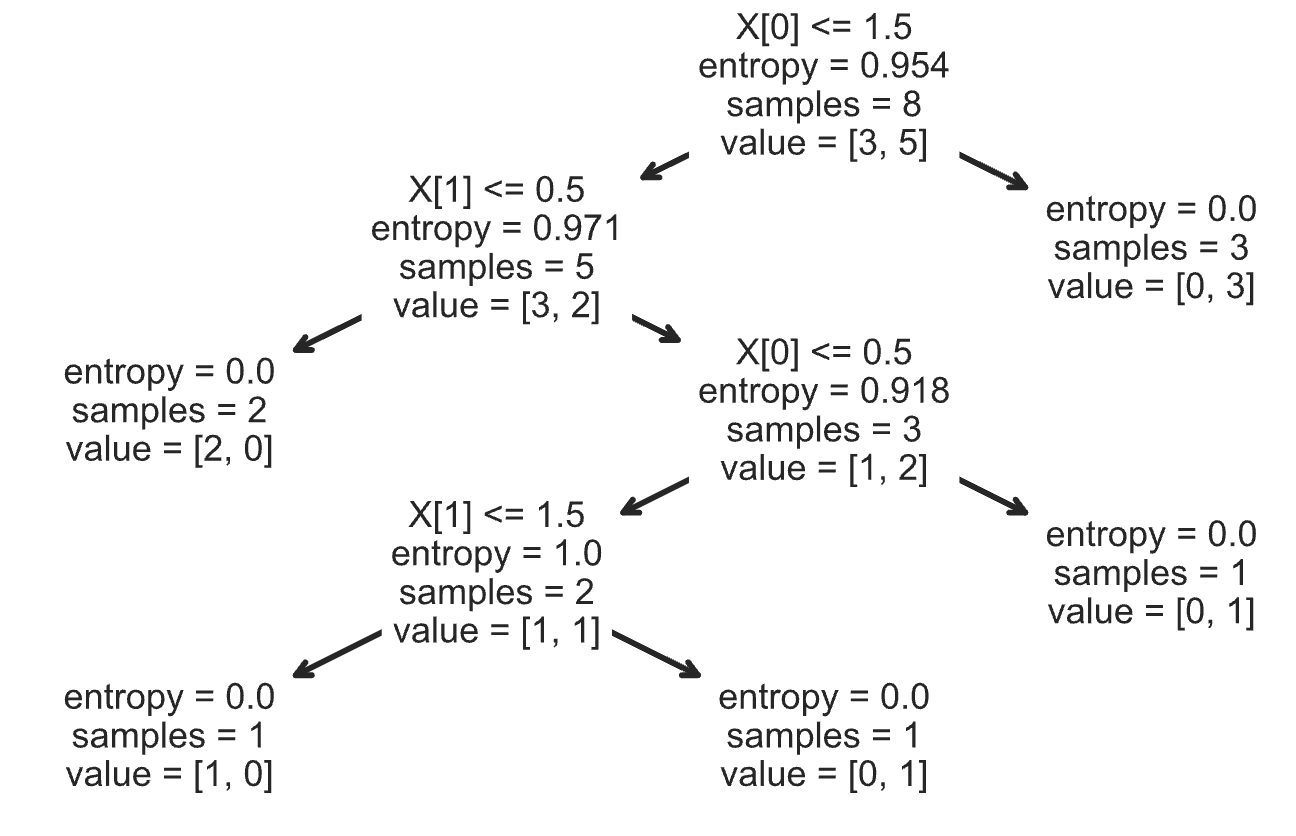
Suppose you fit a decision tree to the training set below, using the features x0 and x1 to predict the outcome y.

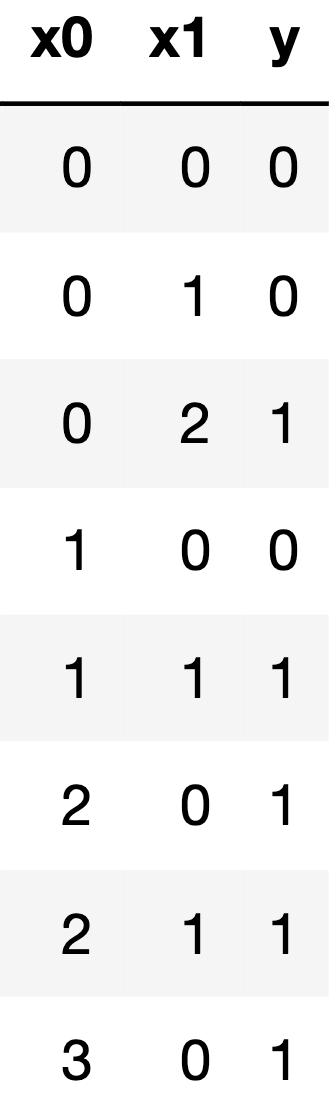
Write the first four splitting rules that are created by the decision tree when fitting this training set (using weighted entropy). Assume that the tree is constructed in a depth-first order. If two candidate splits have the same weighted entropy, choose the one that splits on x0.


Problem 12.1

The first splitting rule is: ___(i)___ <= ___(ii)___

(i):

(ii):

Answer:

(i): x0

(ii): 1



Problem 12.2

The second splitting rule is: ___(i)___ <= ___(ii)___

(i):

(ii):

Answer:

(i): x1

(ii): 0



Problem 12.3

The third splitting rule is: ___(i)___ <= ___(ii)___

(i):

(ii):

Answer:

(i): x0

(ii): 0



Problem 12.4

The fourth splitting rule is: ___(i)___ <= ___(ii)___

(i):

(ii):

Answer:

(i): x1

(ii): 1

Here is a plot of the training data:

Here is a plot of the fitted tree (from scikit-learn):


Problem 13

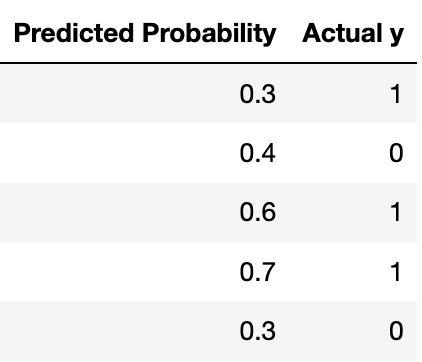
Suppose you fit a logistic regression classifier. The classifier’s predictions on a test set of 5 points are shown below, along with the actual labels.

Recall that for logistic regression, we must also choose a threshold $ \tau $ to convert the predicted probabilities to predicted labels. For this question, assume that $ 0 < \tau < 1 $. Precision is undefined when the classifier doesn’t make any positive predictions (since $\frac{0}{0}$ is undefined). For each question, show your work and draw a box around your final answer in the space provided. Each of your final answers should be a single number.


Problem 13.1

What is the lowest possible precision for any threshold $ \tau $?

Answer:

The lowest precision happens when $ \tau $ is less than 0.3. In this case, the classifier predicts all points are 1, which gives a precision of $ \frac{3}{5} $.



Problem 13.2

What is the lowest possible recall for any threshold $ \tau $?

Answer:

The lowest recall happens when $ \tau $ is greater than 0.7. In this case, the classifier predicts all points are 0, which gives a recall of 0.



Problem 13.3

What is the highest possible recall if the classifier achieves a precision of 1?

Answer:

If precision is 1, the threshold must be greater than 0.4. Of these thresholds, the recall is greatest when the threshold is between 0.4 and 0.6. In this case, the recall is \frac{2}{3}.


👋 Feedback: Find an error? Still confused? Have a suggestion? Let us know here.